数字储能网讯：

摘要

为应对电网形式的转变，促进分布式资源就近消纳，基于数据驱动提出了高比例新能源配电网3层规划模型。决策层采用改进的K-means算法确定负荷中心和分布式电源中心，基于源荷平衡关系划分配电网网格。规划层以综合投资成本最低为目标，对网格内分布式电源和网架结构的修建提出配置方案。运行层模型以综合运行成本最低为目标，促进网格内资源良好互动、网格间资源互济。3层规划模型结合配电网的规划和运行，充分挖掘电源、负荷等多源信息，实现配电网资源上多元联动、空间上网格互动，并通过改进的粒子群算法验证了所提策略的有效性。

1 新型配电网分层规划

为了促进分布式电源的渗透和消纳，采用供电网格区域自治的思想，将配电网分层规划，网格划分原则如图1所示。

图1  配电网格划分层次

Fig.1  Distribution grid division level

1.1  供电网格分层控制体系

新型配电网从物理上划分为区域、网格、台区3层，形成“横纵协同、分层分区”双向协同调控，实现区域优化、网格互济、台区自治的控制体系架构如图2所示，3层相互配合调度配电网全领域的电力管理。

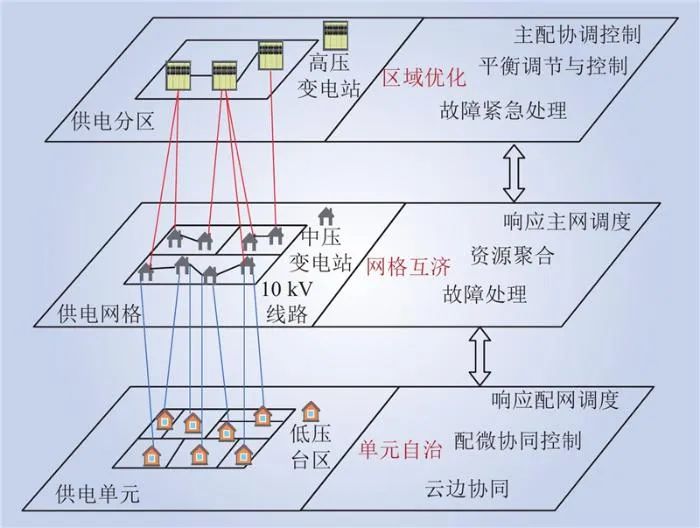
图2  配电网格分层控制体系

Fig.2  Distribution grid hierarchical control system

1）区域优化。供电分区以有功/无功平衡、高可靠性为目标，计算安全运行裕度，调整网格运行方式，调动网格层可调可控资源，紧急情况下指挥多网格内有序用电，实现区域内源荷储之间的最优匹配，保证可靠用电，实现供电分区全局平衡。

2）网格互济。网格层以分布式资源就近消纳为目标，计算网格内中压线路潮流，响应上级区域层的线路运行方式调整，调度单元层可调可控资源，实现网格内分布式资源、储能、负荷之间的最优匹配，实现网格自平衡以及有功协调控制、分布式资源就近消纳、无功电压协同优化和故障处理等功能。

3）单元自治。单元层以自平衡、自治管理为目标，依托智能终端，实现配电台区的数据采集、状况监测和设备监管。支撑台区内分布式资源快速接入、有序运行及配微协同，实现台区源荷储平衡控制和自治运行。

1.2  基于数据驱动的供电网格划分

进行新型配电网规划时，供电网格的划分至关重要。供电网格可基于供电分区下发的分布式资源发电预测以及供电单元上传的发电/负荷预测结果，结合气象信息，实现分布式资源、储能、负荷之间的最优匹配。

供电网格还可通过线路及台区间的转供、串供、站内联络等负荷转供手段，响应区域层线路运行方式调整，实现不同电源点、不同线路之间的灵活调整和功率互济，增强配电网故障后的自愈恢复能力。

本文通过数据驱动方法分析历史用电数据、人口分布、经济发展水平、地理信息等多维度数据，精准地识别用电需求特征和负荷分布规律，从而指导供电网格的合理划分，确保网格内的资源得到优化配置。

2 新型配电网三层规划模型

本文基于数据驱动建立决策-规划-运行三层优化模型。决策层以分布式资源渗透率差值最低为目标，以现有分布式资源分布和负荷分布为决策变量，划分供电网格。规划层以供电网格为单位，以规划投资成本、供电可靠性为目标，以分布式资源和网架线路的修建为决策变量，制定规划方案。运行层在规划层的决策下，以经济运行成本和环境污染成本最小为目标，以分布式资源出力情况、污染物排放量、储能容量作为决策变量，配置最优运行方案。模型框架如图3所示。

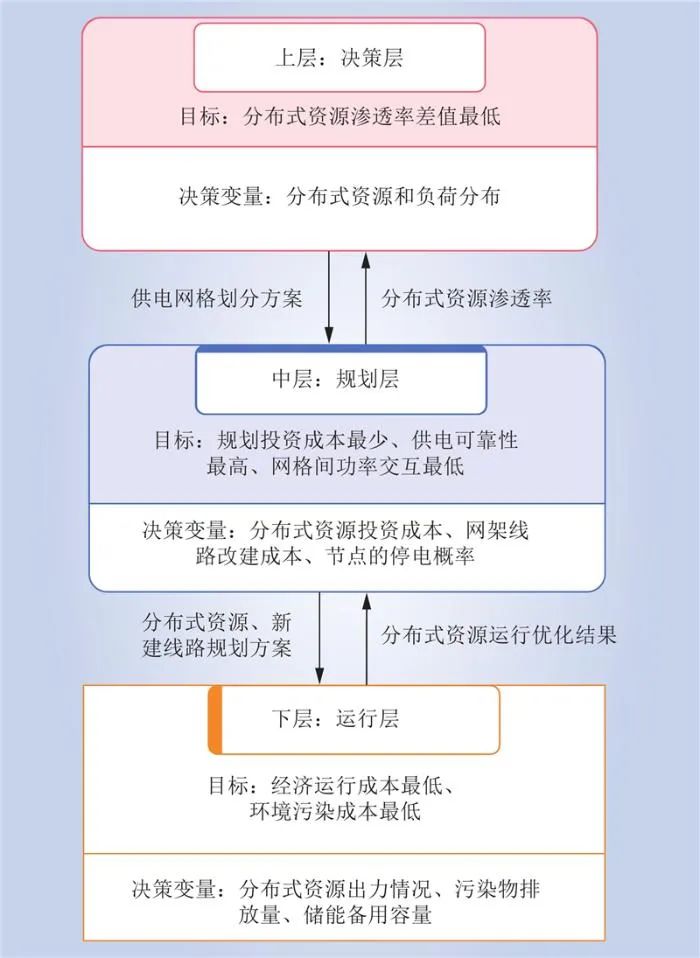
图3  新型配电网三层规划模型

Fig.3  Three-layer planning model of new distribution network

2.1  决策层模型

1）分布式资源渗透率差值f1为

式中：N为网格数量；PG为供电分区中的电源出力；PD为供电分区中的负荷有功功率；PG,m为第m个网格的电源出力；PD,m为第m个网格的负荷有功功率。

2）网络i的负荷中心和电源中心距离f2,i为

式中：xdm,i、ydm,i分别为第m个网格中第i个负荷中心的横纵坐标；xgm,i、ygm,i分别为第m个网格中第i个电源中心的横纵坐标。

约束条件包括线路负载率约束、供电半径约束。

2.2  规划层模型

1）规划投资成本为

式中：Ceco为网格规划策略投资总费用；ε为维护运行费用系数和投资折旧的回收系数之和；Cij,m为第m个站间网格中主干线路ij的投资成本；Cfij,n为第n个非站间网格中环网线路ih的投资成本； Cfs,n为第n个非站间网格中辐射状线路的投资成本；为第m个站间网格的主干线路ij电能年损耗费用；为第n个非站间供电网格的主干线路年损耗费用；Cin为分布式资源投资建设成本；Cl为网格间数字化联络投资；Nij为站间供电网格ij数量；Nfij为非站间供电网格数量。

将数字化联络规划考虑到稳态网格划分中，合理的数字化联络设施有利于提高配电网的网格控制效果。数字化联络设施由数据传输线以及网格控制单元组成。对数字化联络设施做如下假设：联络线路沿电力线路架设，同时各个节点均存在数字化联络子站，且联络子站离变电站的距离不远。设置数字化联络投资Cl为

式中：dm为网格m的支路线长；pl为数据传输线单价；pc为网格控制单元单价。

2）供电可靠性为

式中：Clos为配电网可靠性指标；Plo,m,j为第m个网格中j节点的停电概率；Nlos为停电次数；t 为停电持续时间；J为节点数量；Sm,j为第m个网格中j节点的供电状态；Pm,j(t)为t时刻第m个网格内j节点的实际功率。

3）网格m、n间功率交互Em,n为

式中：Pij、Qij分别为网格间支路ij的有功以及无功潮流；ncl为网格数；k为网格间支路数；Pp、Pq分别为有功/无功交互系数；Ps为支路系数。

约束条件包括配电网潮流约束、节点电压约束。

2.3  运行层模型

网格经济运行成本为

式中：Cf为供电网格一天内的经济运行成本；Cop为一天内分布式资源运行维护总成本；Cpro为分布式资源总收益；COM为各网格的运行总管理成本； Cbuy、Csell分别为供电网格与电网之间的总购电支出与售电收益；Cwt、Cpv、Cmt、Cfc、Cess分别为风力发电机、光伏电池、微型燃气轮机、燃料电池以及储能的总运行成本。

约束条件包括网格功率平衡约束、各分布式电源功率约束、储能容量约束等。

3 模型求解

K-means算法是一种基于目标函数的聚类算法，该算法通常采用欧氏距离作为供电网格划分依据。区域划分综合指标体系主要由县域配电网的划分目标和原则决定。本文以降低电压波动的峰值和减少净负荷的波动幅度为目标，在这一基础上，同时考虑到区域的功能性需求，构建了一个综合性的指标体系。这个体系旨在全面评估和优化配电网的区域划分，从而最大化配电网的区域自治能力。

改进的K-means算法是一种基于聚类数k的硬聚类算法，其具体步骤如下。

1）以网格划分的前置条件，确定分区聚类数k。

2）确定归类的条件，将负荷点、分布式资源的时空距离作为归类条件。

3）根据区域划分综合指标计算权重。权重越小，表示数据点之间的相似性越大。

4）使用最小权匹配算法，找到图中的最小权重集合，将数据点分成不同的组。

5）通过K-means算法分别选出聚类中心和负荷中心。

6）最小权匹配的边会连接两个属于不同聚类的顶点，把相近的聚类中心和负荷中心进行优化匹配，确定网格划分结果。

粒子群优化算法是通过更新粒子群的速度和位置，不断迭代寻找粒子群的最优适应度达到寻优目的。但在迭代求解过程中，由于种群多样性不足，易陷入局部解；为了解决这个问题，本文在迭代过程中引入高斯变异方法，增加种群的多样性，避免陷入局部最优。

神经网络算通常需要多次迭代才能收敛到最优或近似最优解。迭代次数越多，算法的运行时间也越长。为了提高计算效率，本文采用数据并行的神经网络算法，将大规模数据集分割成多个小批次，然后在多个计算单元上同时进行训练。

本文所述3层规划模型求解流程如图4所示。决策层采用改进的K-means算法划分供电网格。规划层和运行层采用改进的粒子群算法和优化的数据驱动方法确定最优规划方案。

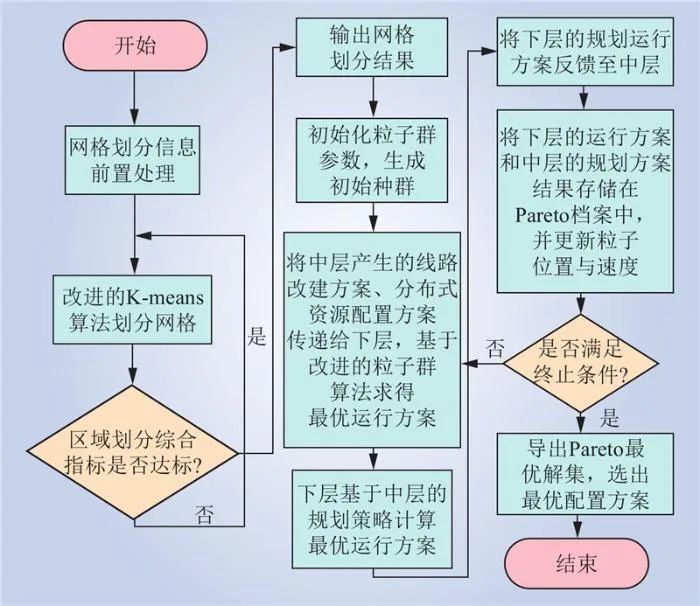
图4  新型配电网3层规划模型求解流程

Fig.4  Solution flow of three-layer planning model for new distribution network

4 算例分析

为验证所提策略的有效性，在Matlab上以IEEE 33节点为例进行仿真实验。系统基准电压取12.66 kV，节点电压允许区间为 [0.95, 1.05] p.u.，系统内已配置柴油机组，拟配置分布式电源类型包括风机、光伏、微型燃气轮机、燃料电池以及储能装置。单台分布式电源的额定容量为50 kW，单位容量投资成本分别为5000、6500、1500、4500、2000元/kW；单位维护成本为0.06、0.04、0.04、0.001、0.05元/(kW·h)，线路单位长度投资成本为20万元/km，规划投资年限为10年，折现率为0.1。每个节点接入风机和光伏设备数量最多为10台。储能设备荷电量为[0.1, 0.9]，充放电效率为0.9。低谷时段00:00—08:00、11:30—13:30购电电价为0.25元/(kW·h)；平段08:00—11:30、13:30—16:30、22:30—24:00购电电价为0.42元/(kW·h)；峰段16:30—20:30购电电价为0.65元/(kW·h)；尖峰时段20:30—22:30购电电价为0.82元/(kW·h)。

4.1  仿真结果

基于本文提出的规划模型，改进的K-means算法求解出的网格划分结果如图5所示。采用贵州某地典型日实际的风光荷数据如图6所示。

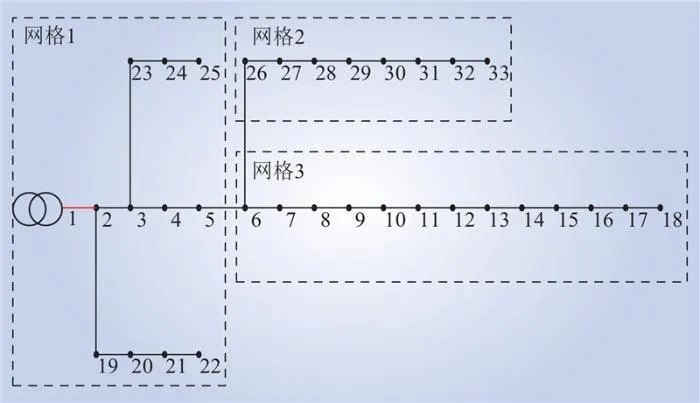
图5  配电网网格划分结果

Fig.5  Distribution grid division results

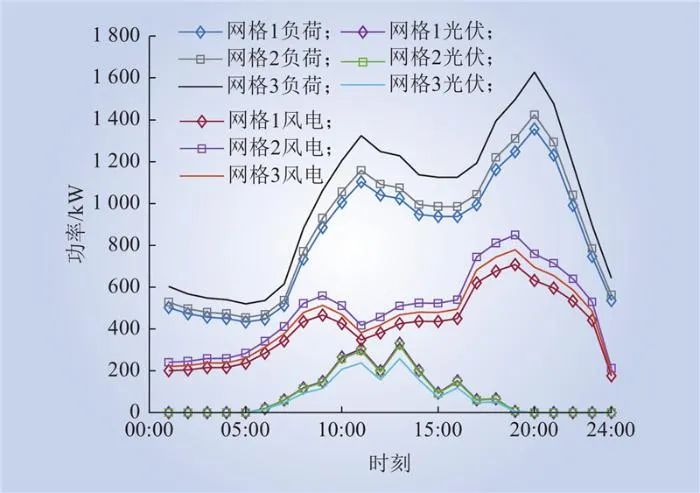
图6  典型日负荷和风光出力场景

Fig.6  Typical daily load and wind/PV output scene

初始参数设置：初始种群规模为80，迭代次数为100次。设定分布式能源发电占总发电量的50%以上。针对分布式资源的不确定特性，在配置规划中倾向于将其布置于负载密集区域，旨在实现资源的就近消纳。考虑到光伏的不确定性，储能设备应配置于分布式光伏较为集中的区域，通过充放电达到削峰填谷的目的，提升配电网的稳定性。其规划方案如表1所示。

表1  配电网规划方案

Table 1  Distribution network planning scheme

根据规划方案求解出的典型日最优运行方案如图7~9所示。综合图7~9可得，各区域在风光大发时，储能设备进行充电，并在用电高峰期间，将电能出售给电网，在低谷期进行购电和储能设备充电，实现对分布式资源的就近消纳，同时利用峰谷期的电价差实现运行成本的最小化。

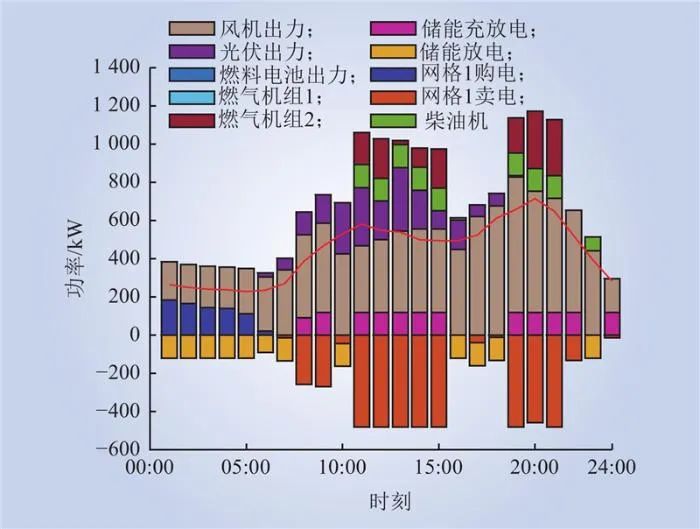
图7  供电网格1典型日运行情况

Fig.7  Power grid 1 typical daily operation

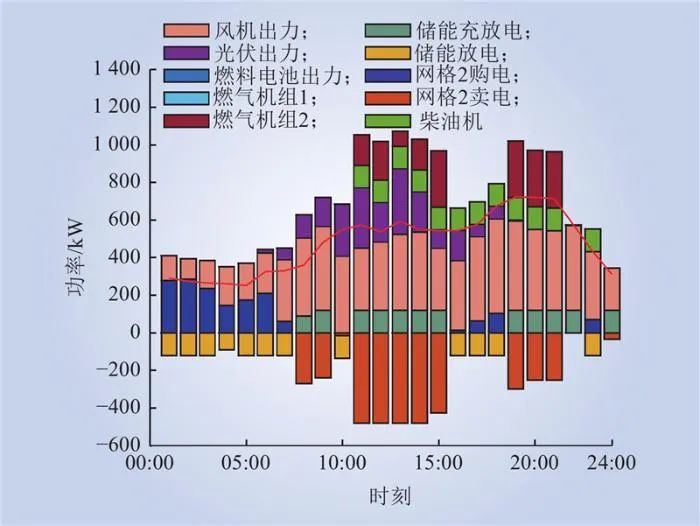
图8  供电网格2典型日运行情况

Fig.8  Power grid 2 typical daily operation

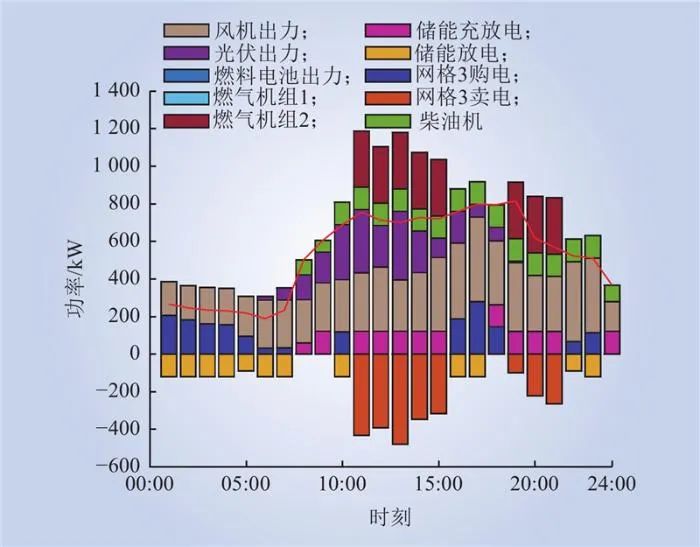
图9  供电网格3典型日运行情况

Fig.9  Power grid 3 typical daily operation

4.2  仿真结果敏感性分析

为了校验本文所提规划模型的优势，设置以下3种方案进行分析对比：方案1为根据《指导原则》确定的规划方案；方案2为采用集中式的资源布局，没有考虑分布式资源的地理位置和分布特性；方案3为本文所提的3层规划模型。比较结果如图10所示，相比方案1、方案2，方案3的成本和电压偏差都有所降低，说明该规划经济性和可靠性都得到了优化。这是因为传统方法未充分考虑各区域分布式资源的禀赋，导致弃风弃光现象严重；而方案3改善了分布式资源在时间与空间维度上的不平衡，并充分利用电价差实现最优调度，提升了规划方案的经济性和可靠性。

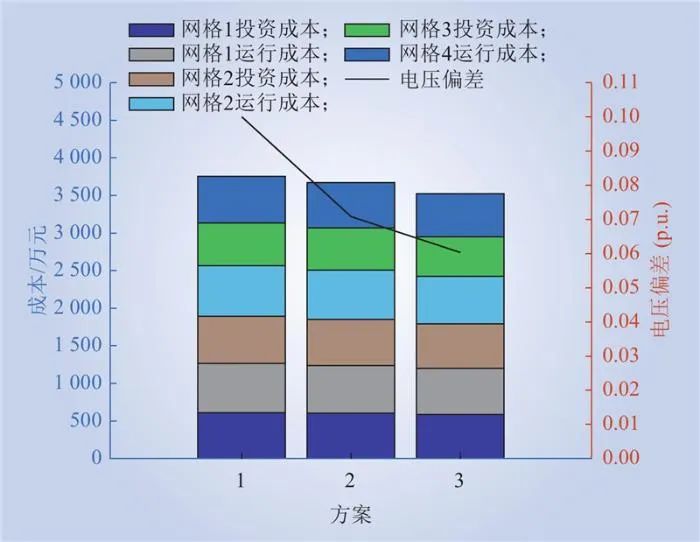
图10  不同方案规划结果对比

Fig.10  Comparison of planning results of different schemes

5 结论

为响应新形势下配电网的转型，本文以新型配电网为例，构建了3层规划模型，主要结论如下。

1）在决策层，基于数据驱动深度融合地区的负荷分布、分布式资源、常规火力发电机组的出力情况和电网运行数据，依据源荷平衡对供电分区进行网格划分，降低规划维度。

2）在规划层，为提升经济效益，保障电力安全可靠，强化源网荷储协同发展，满足分布式新能源发展需要，须结合地理空间数据、用户需求、经济指标等大数据，科学地规划电网布局，优化电网结构，确保新建设施满足未来负荷增长和可再生能源接入的需求。

3）在运行层，灵活调用分布式发电、储能和需求侧响应等各项资源，促使供电网格内资源良好互动，网格间资源互济，进而提高分布式资源消纳率，降低网损。

本文所提方法综合考虑了规划区域的分布式资源渗透率、电网的经济性和安全性，降低了规划的维度和难度，提升了规划的精度，为后续加快配电网建设改造和智慧升级、强化源网荷储协同发展提供助力。